1079. Удаление букв
Вам задано два слова, каждое из которых состоит из
заглавных английских букв. Удалите из них несколько букв так, чтобы в
результате получились одинаковые слова.
Найдите максимально возможную длину полученного слова.
Вход. Каждый тест состоит из одной строки, содержащей два
заданных слова, разделенных пробелом. Длина каждого слова от 1 до 200 символов.
Всего имеется не более 10 тестов.
Выход. Для каждого
теста выведите максимально возможную длину полученных одинаковых слов (длину
максимального слова, которое можно получить путем удаления некоторых букв).
Если одинаковые
слова получить невозможно, то выведите 0.
|
Пример
входа |
Пример
выхода |
|
AAABBB ABABAB AXYAAZ CXCYCZC ABCDE EDCBA |
4 3 1 |
РЕШЕНИЕ
динамическое
программирование - НОП
Анализ алгоритма
Ответом задачи
будет длина наибольшей общей подпоследовательности (НОП) входных последовательностей заглавных латинских букв.
Пусть f(i,
j) – длина наибольшей общей подпоследовательности последовательностей x1x2…xi
и y1y2…yj.
Если xi ¹ yj, то ищем НОП среди x1x2…xi-1 и y1y2…yj,
а также среди x1x2…xi и y1y2…yj-1. Большую из них возвращаем:
f(i, j) = max( f(i,
j – 1), f(i – 1, j) )
Если xi = yj, то ищем
НОП среди x1x2…xi-1 и y1y2…yj-1:
f(i, j) = 1 + f(i –
1, j – 1)
Значения f(i,
j) будем хранить в массиве m[0.. SIZE, 0.. SIZE], где m[0][i] = m[i][0] = 0. Поскольку длины
слов не более 200 символов, то положим SIZE = 201.
Каждая следующая
строка массива m[i][j] вычисляется через предыдущую. Поэтому для
нахождения ответа достаточно держать в памяти только две строки.
Пример
Приведем наибольшие
общие подпоследовательности для заданных примеров.
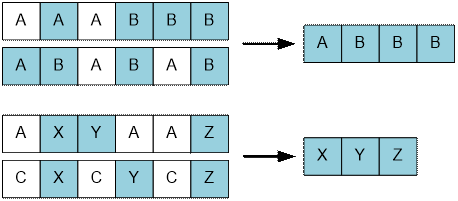
Реализация алгоритма
Строки x
и y содержат входные последовательности, lenx и leny – их
длины. Массив m содержит две последние строки динамического
преобразования.
#define SIZE 1001
string x, y;
int m[2][SIZE];
int lenx, leny;
Входные данные
обрабатываем, пока не встретится конец файла. Читаем две входные
последовательности в строки x и y. К строкам спереди припишем пробел,
чтобы последовательности начинались с первой ячейки. Позиции последних символов
строк сохраняем в переменных lenx и leny.
while (cin >> x >> y)
{
x = ' ' + x; lenx = x.size() - 1;
y = ' ' + y; leny = y.size() - 1;
Обнуляем массив m.
Динамически вычисляем значения f(i, j). Изначально m[0][j]
содержит значения f(0, j). Далее в m[1][j] заносим
значения f(1, j). Поскольку для вычисления f(2, j) достаточно
иметь значения двух предыдущих строк массива m, то значения f(2, j)
можно сохранять в ячейках m[0][j], значения f(3, j) – в
ячейках m[1][j] и так далее.
memset(m,0,sizeof(m));
for(i = 1; i <=
lenx; i++)
for(j = 1; j <=
leny; j++)
if (x[i] ==
y[j]) m[i % 2][j] = 1 + m[(i-1)%2][j-1];
else m[i %
2][j] = max(m[(i-1)%2][j],m[i%2][j-1]);
В конце
алгоритма длина наибольшей общей подпоследовательности будет находиться в
ячейке m[lenx%2][leny]. Выводим ее.
cout << m[lenx % 2][leny] << endl;
}